Paix.....!
Alors G. tu connais peut-être le passage de 1 Rois 7:23 ... de fait l'idée a été reprise par entres autres Armel Larochelle Astrophysicien Canadien dans un livre dont le titre est très clair :
Pi = 3.
En fait dans l'Antiquité ( où il n'y avait pas d'informatique, pas d'outils d'extrême précision... ) on cherchait surtout à entourer le nombre Pi sa limite inférieure et sa limite supérieure ;
c'est à dire que Pi était un nombre forcément compris entre 3 et 3.2 par exemple....
Ensuite de plus en plus proche entre 3 et 3.15...ensuite entre 3 et 3,14 etc etc....
========================================================
De ceci on peut se demander s'il n'y a pas eu une confusion au cours du temps ; de sorte que la limite supérieure de Pi ( 3,14.....) a fini par être considérée elle-même par Pi.....??
========================================================
Cette résolution de la quadrature du cercle part donc du principe que la nature que les lois de la nature de l'univers sont FONDAMENTALEMENT simples et logiques ( Cf Rasoir d'Ockham ).
Nous partons donc du principe que 3.14... n'est pas le nombre Pi lui même mais simplement sa limite supérieure et donc que Pi = 3.
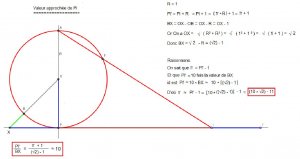
1). L'aire d'un cercle C par exemple de rayon R est donc :
======================================
A = 3 R²
2) Tout devient si simple et si logique...!
===========================
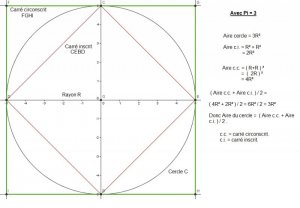
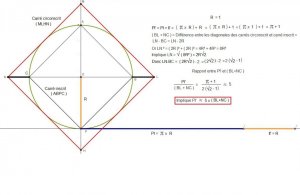
° L'Aire donc du carré inscrit dans le cercle C est
Aire ci = R² + R² = 2R².
° L'Aire du carré qui entoure le cercle ( carré circonscrit ) est :
Aire cc = ( 2R )² = 4R²
3) Maintenant si nous additionnons l'Aire du carré inscrit et l'aire du carré circonscrit qu'obtenons nous..??
====================================================================
Aire carré inscrit = 2R²
Aire carré circonscrit = 4R²
Aire carré inscrit + Aire carré circonscrit = 2R² + 4R² = 6R²
Or 6R² est égal au double de l'aire du cercle donc nous voyons tout simplement que l'aire du cercle C est la MOYENNE entre l'aire du carré inscrit et le carré circonscrit :
Aire Cercle C = ( Aire carré inscrit + Aire carré circonscrit ) / 2
3R² = ( 2R² + 4R² ) / 2.
Donc voilà nous avons notre Quadrature.....!
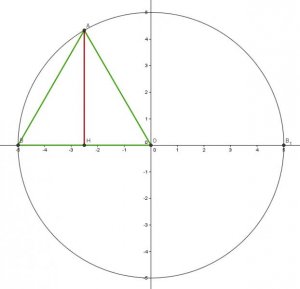
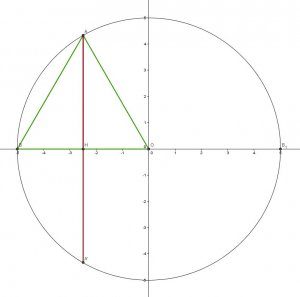
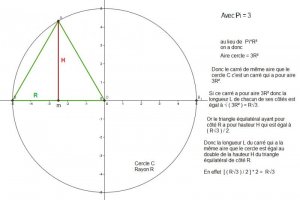
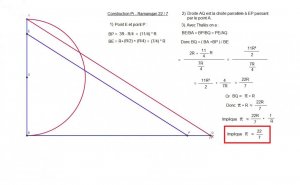
4) Ce que nous pouvons retrouver également grâce au triangle équilatéral de côté R ( c'est à dire le rayon du cercle ).
============================================================================
En effet nous avons l'aire du cercle c de rayon R =
Aire C = 3R²
Donc la Longueur L du carré ayant même aire que le cercle C de rayon R est :
L = √ ( 3R²) = R√3
Or nous pouvons voir que R√3 est tout simplement le double de la Longueur de la hauteur du triangle Équilatéral de côté R......!
En effet dans ce triangle équilatéral de côté R la hauteur est égal à :
( R√3 ) / 2 et donc le double de cette hauteur donne bien la Longueur L du carré recherché :
[( R√3 ) / 2] * 2 = R√3
Nous voyons donc que Pi = 3 nous retrouvons une logique une simplicité et un recoupement des valeurs particulières relatives au cercle et aux autres figures géométriques.....!
Voilà G. on peut donc se demander si avec le temps il n'y à pas eu une confusion entre le nombre Pi et sa limite supérieure, ce fameux 3.14 que l'on a fini par assimiler à Pi lui-même.
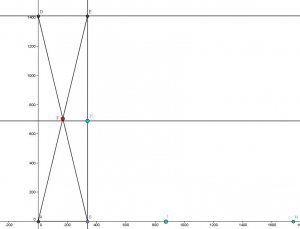
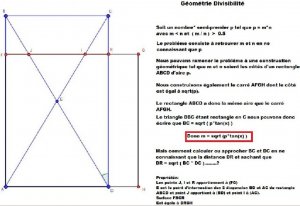
Les graphiques sont joints au post.
Alors G. tu connais peut-être le passage de 1 Rois 7:23 ... de fait l'idée a été reprise par entres autres Armel Larochelle Astrophysicien Canadien dans un livre dont le titre est très clair :
Pi = 3.
En fait dans l'Antiquité ( où il n'y avait pas d'informatique, pas d'outils d'extrême précision... ) on cherchait surtout à entourer le nombre Pi sa limite inférieure et sa limite supérieure ;
c'est à dire que Pi était un nombre forcément compris entre 3 et 3.2 par exemple....
Ensuite de plus en plus proche entre 3 et 3.15...ensuite entre 3 et 3,14 etc etc....
========================================================
De ceci on peut se demander s'il n'y a pas eu une confusion au cours du temps ; de sorte que la limite supérieure de Pi ( 3,14.....) a fini par être considérée elle-même par Pi.....??
========================================================
Cette résolution de la quadrature du cercle part donc du principe que la nature que les lois de la nature de l'univers sont FONDAMENTALEMENT simples et logiques ( Cf Rasoir d'Ockham ).
Nous partons donc du principe que 3.14... n'est pas le nombre Pi lui même mais simplement sa limite supérieure et donc que Pi = 3.
1). L'aire d'un cercle C par exemple de rayon R est donc :
======================================
A = 3 R²
2) Tout devient si simple et si logique...!
===========================
° L'Aire donc du carré inscrit dans le cercle C est
Aire ci = R² + R² = 2R².
° L'Aire du carré qui entoure le cercle ( carré circonscrit ) est :
Aire cc = ( 2R )² = 4R²
3) Maintenant si nous additionnons l'Aire du carré inscrit et l'aire du carré circonscrit qu'obtenons nous..??
====================================================================
Aire carré inscrit = 2R²
Aire carré circonscrit = 4R²
Aire carré inscrit + Aire carré circonscrit = 2R² + 4R² = 6R²
Or 6R² est égal au double de l'aire du cercle donc nous voyons tout simplement que l'aire du cercle C est la MOYENNE entre l'aire du carré inscrit et le carré circonscrit :
Aire Cercle C = ( Aire carré inscrit + Aire carré circonscrit ) / 2
3R² = ( 2R² + 4R² ) / 2.
Donc voilà nous avons notre Quadrature.....!
4) Ce que nous pouvons retrouver également grâce au triangle équilatéral de côté R ( c'est à dire le rayon du cercle ).
============================================================================
En effet nous avons l'aire du cercle c de rayon R =
Aire C = 3R²
Donc la Longueur L du carré ayant même aire que le cercle C de rayon R est :
L = √ ( 3R²) = R√3
Or nous pouvons voir que R√3 est tout simplement le double de la Longueur de la hauteur du triangle Équilatéral de côté R......!
En effet dans ce triangle équilatéral de côté R la hauteur est égal à :
( R√3 ) / 2 et donc le double de cette hauteur donne bien la Longueur L du carré recherché :
[( R√3 ) / 2] * 2 = R√3
Nous voyons donc que Pi = 3 nous retrouvons une logique une simplicité et un recoupement des valeurs particulières relatives au cercle et aux autres figures géométriques.....!
Voilà G. on peut donc se demander si avec le temps il n'y à pas eu une confusion entre le nombre Pi et sa limite supérieure, ce fameux 3.14 que l'on a fini par assimiler à Pi lui-même.
Les graphiques sont joints au post.