AbuBatata
DANIEL GALVAN FAN CLUB
Bon je donne la solution:
E est l'ensemble des entiers tel que :
p(n)<= (1/n) * (p(0) + ... + p(n))
=>
p(0) >= (p(n)-p(n)) + ... + (p(n)-p(1))
Or notre serie est strictement croissante donc si n>i alors p(n)-p(i)>=1
Donc p(0) >= n - 1
Ce qui force E a etre fini
Soit m=Max(E)
Forcement m+1 n'est pas dans E
Donc p(m+1) > (1/m) * (p(0) + ... +p(m))
Et c'est fini
Elle est pas belle ma demo
Turlututu mon chaton, on est pas ici pour faire tes devoirs de maths....
A cause de toi j'ai du rouvrir Wolfram Alpha en pleine vacance d'été... Une première. Par contre j'avoue avoir buté sur la série quoique ton explication est convaincante.
Des défis, des défis, des défis !
A moi :
C'est un projet sur lequel j'ai bossé un peu plus de 6 mois. Je devais trouver le modèle représentant le mieux la démultiplication ou pas du défaut sur une pale de turbine de réacteur d'avion (A3*0) après de nombreux test.
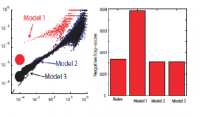
Ci dessous un graphique représentant l'évolution d'un défaut structurelle dit "interne" à un turbine de palier de réacteur. Le défaut est révélé via ionisation, ressuage, magnétoscopie etc. Un petit défaut sur ce type de palier peut entraîner la casse de ce dernier, la destruction du compresseur voir une décompression explosive de l'appareil suite à un choc avec des élément du réacteur. Ca c'est le gâteau.
Quel a été le modèle utilisé, se rapprochant le plus de ce data ?
Indice: -log-score négatif -Pourcentage d'erreur de calibration à 0.01% -Axe y (Estimation empirique du défaut) (Yn) -Axe x (Prévision d'apparition du défaut) (Pn)
NL(y,p)=............................................................
Certains penserons qu'il manque des donnés je suis d'accord, mais essayer de vous rapprocher du modèle énoncé, je demande pas de trouver le modèle exact, mais celui s'approchant le plus.